https://leetcode.com/problems/validate-ip-address/
Validate IP Address - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
LeetCode 문제를 풀었는데 처음으로 Runtime이 100%만큼의 축적된 다른 답안들 보다 빠르다고 나옴

신기해서 자세히 보니

총 73,968 명이 답을 했는데 그중에 C++ 만 대략 50~80명 낸듯;;


메모리는 92.27% 답안들 보다 덜 쓴다고 나옴
사실 내 답안이 제일 하위권에 속할 줄 알았는데 의외의 결과 였음
그래도 실력이 향상됐다는 기록이기도 해서 올려봄
코드
class Solution {
public:
bool IsValidInteger(char *_str)
{
if (atoi(_str) > 255)
{
return false;
}
if (_str[0] == '0' && strlen(_str) > 1)
{
return false;
}
for (int i = 0; i < strlen(_str); i++)
{
char c = _str[i];
if (c >= '0' && c <= '9')
{
continue;
}
else
{
return false;
}
}
return true;
}
bool IsValidHexadecimal(char* _str)
{
if (_str[0] == '0' && strlen(_str) > 4 )
{
return false;
}
if (strlen(_str) > 4)
{
return false;
}
for (int i = 0; i < strlen(_str); i++)
{
char c = _str[i];
bool InValidtest1 = c < '0' || c > '9';
if (InValidtest1)
{
bool InValidtest2 = (c < 'a' || c > 'f'); // c가 'a' 보다 작거나, 'f' 보다 크다
bool InValidtest3 = (c < 'A' || c > 'F'); // c가 'A' 보다 작거나, 'F' 보다 크다
if (InValidtest2 && InValidtest3)
{
return false;
}
}
}
return true;
}
string validIPAddress(string IP) {
bool validIPv4 = true;
bool validIPv6 = true;
//1.IPv4 모양인지 아니면 IPv6 모양인지 검사
//최대 갯수 넘어가는지 검사
if (IP.length() > 15 || IP.length() < 7)
{
validIPv4 = false;
}
if (IP.length() > 39 || IP.length() < 15)
{
validIPv6 = false;
if (!validIPv4)
{
return "Neither";
}
}
// . 갯수 검사
size_t tokenCount = 0;
for (size_t i = 0; i < IP.length(); i++)
{
if (IP.c_str()[i] == '.')
{
tokenCount++;
}
}
if (tokenCount != 3)
{
validIPv4 = false;
}
// : 갯수 검사
tokenCount = 0;
for (size_t i = 0; i < IP.length(); i++)
{
if (IP.c_str()[i] == ':')
{
tokenCount++;
}
}
if (tokenCount != 7)
{
validIPv6 = false;
}
int chunkCount = 0;
if (validIPv4)
{
char IPv4[16] = { 0 };
strcpy(IPv4, IP.c_str());
char* tok = strtok(IPv4, ".");
chunkCount++;
while (tok != nullptr)
{
if (IsValidInteger(tok) == false)
{
validIPv4 = false;
break;
}
else
{
tok = strtok(NULL, ".");
if (tok)
{
chunkCount++;
}
}
}
if (chunkCount != 4)
{
validIPv4 = false;
}
}
else if (validIPv6)
{
char IPv6[40] = { 0 };
strcpy(IPv6, IP.c_str());
int chunkCount = 0;
char* tok = strtok(IPv6, ":");
chunkCount++;
while (tok != nullptr)
{
if (IsValidHexadecimal(tok) == false)
{
validIPv6 = false;
break;
}
else
{
tok = strtok(NULL, ":");
if (tok)
{
chunkCount++;
}
}
}
if (chunkCount != 8)
{
validIPv6 = false;
}
}
if (validIPv4)
{
return "IPv4";
}
else if (validIPv6)
{
return "IPv6";
}
else
{
return "Neither";
}
}
};'자료구조&알고리즘' 카테고리의 다른 글
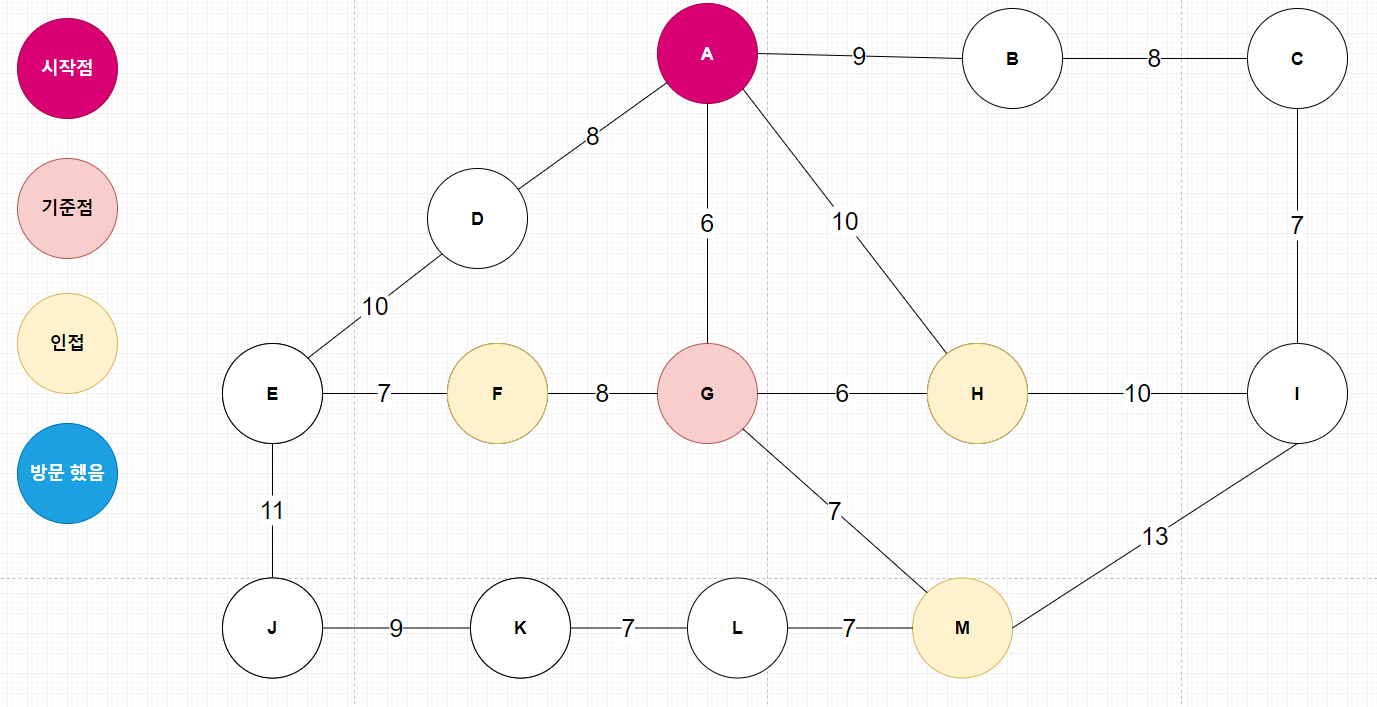
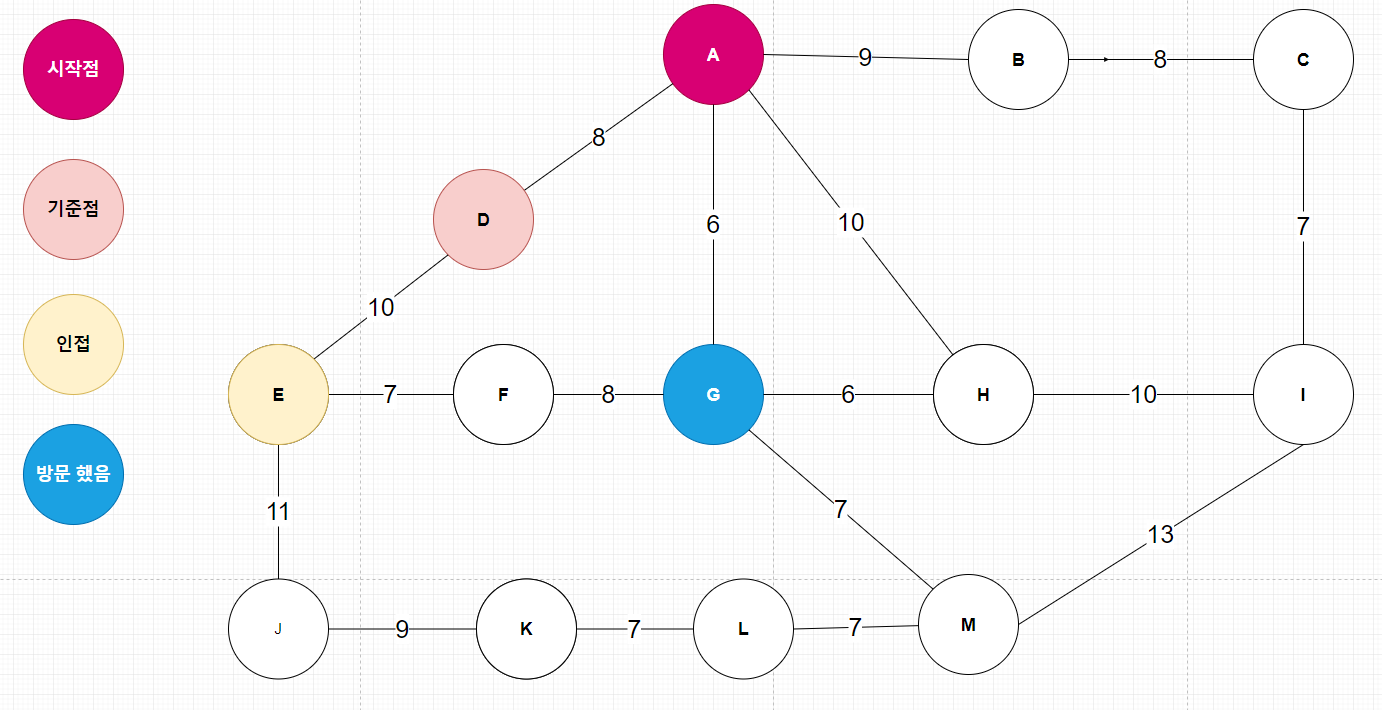
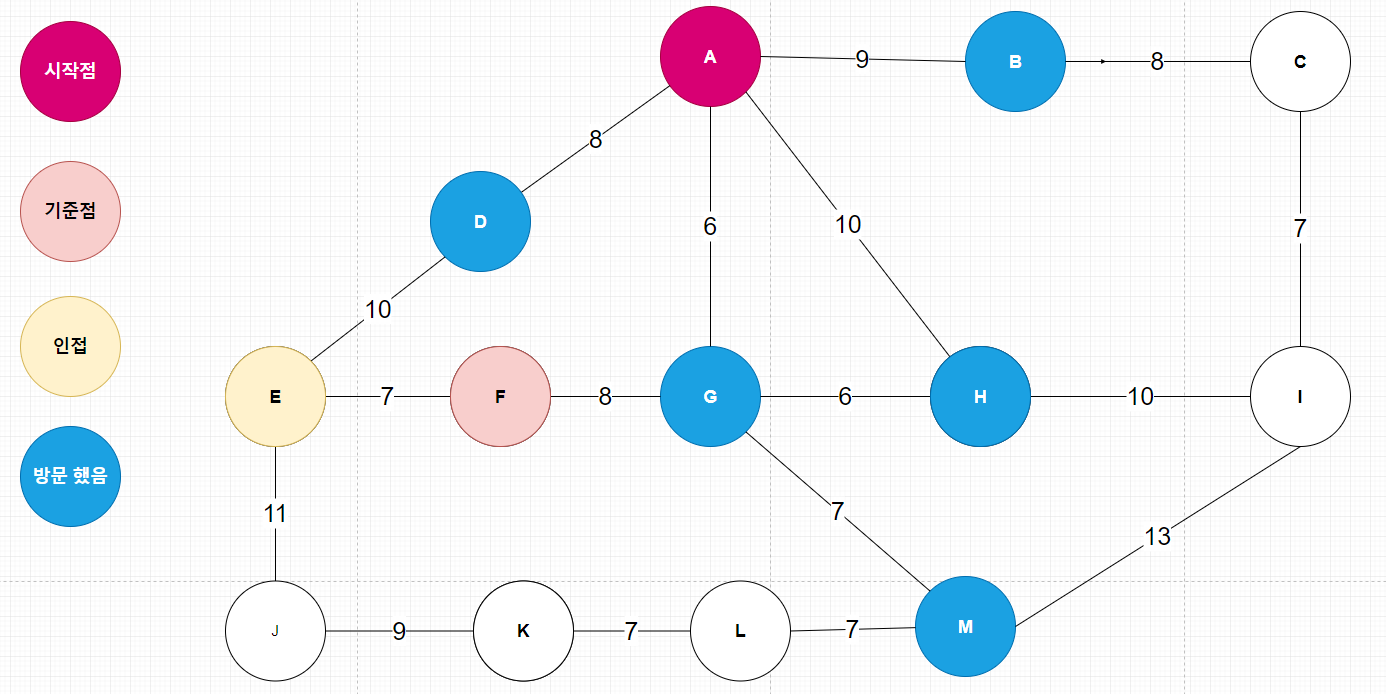
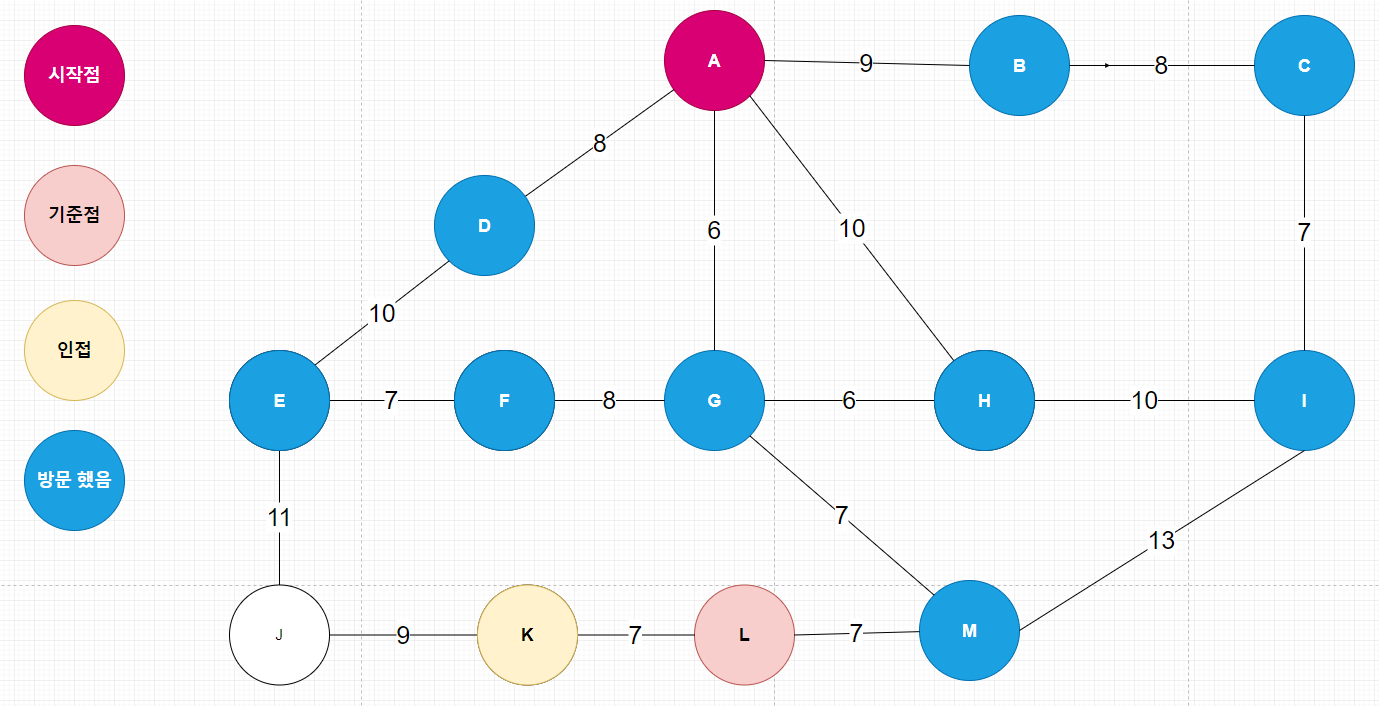
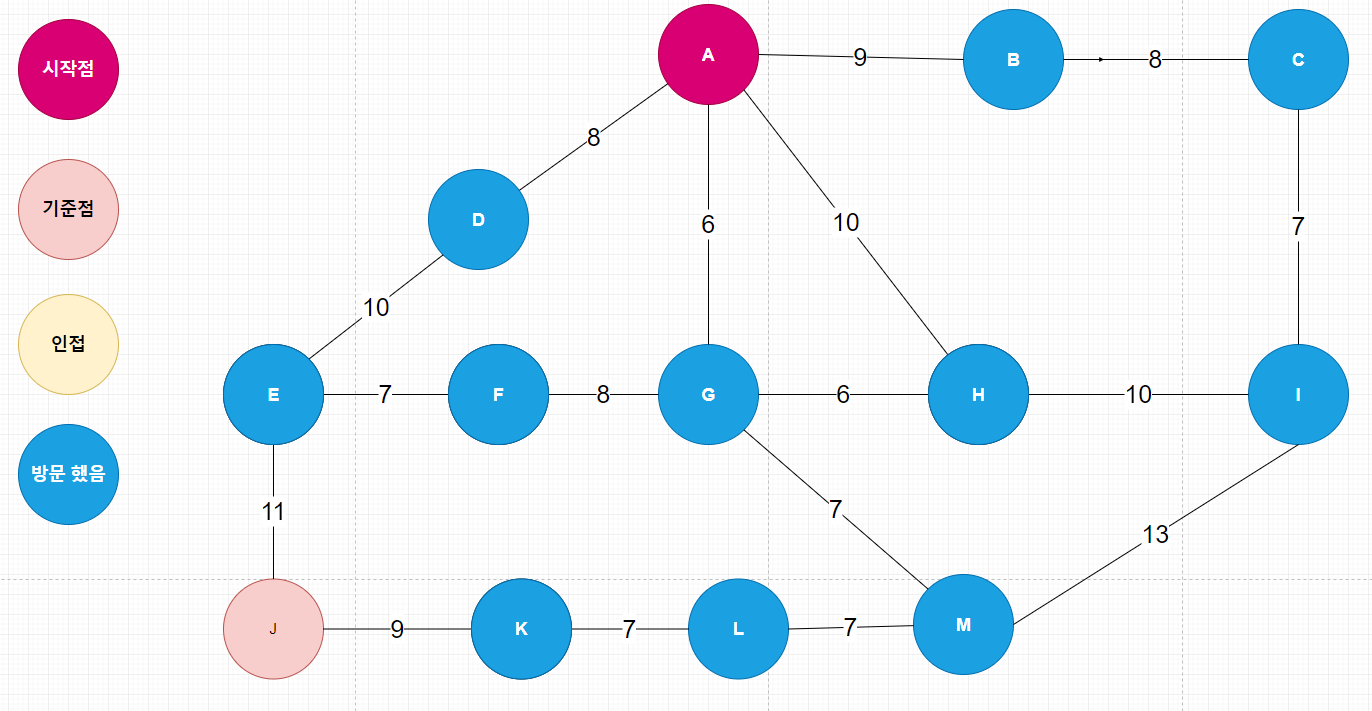
| 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2020.06.08 |
|---|---|
| 에라토스테네스의 체, The Sieve of Erathosthenes (0) | 2020.06.07 |
| Priority Queue(우선 순위 큐), Heap(Max Heap, Min Heap) (0) | 2020.04.12 |
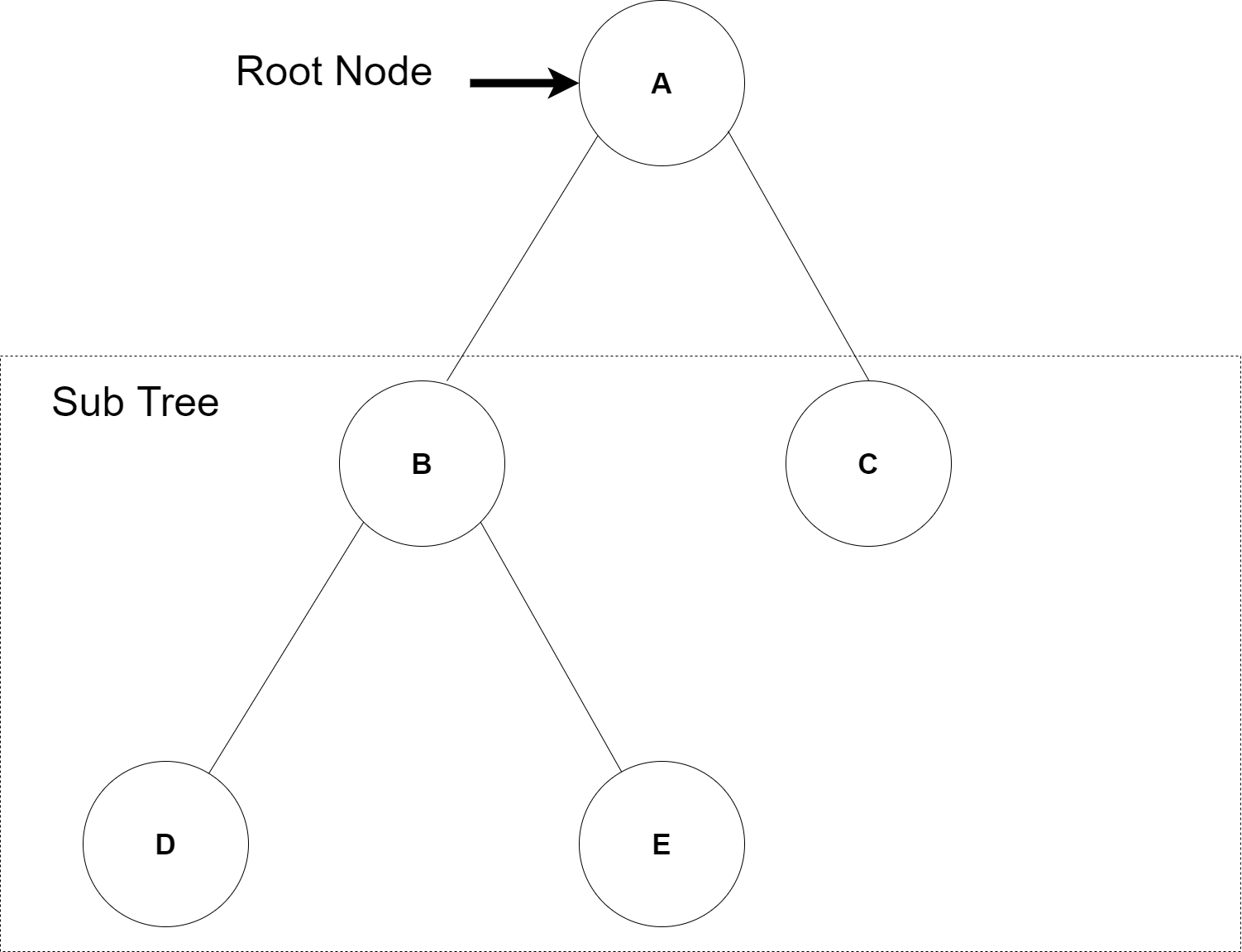
| Tree (0) | 2020.04.09 |
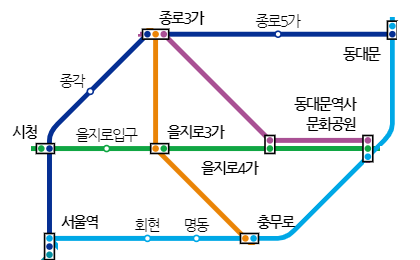
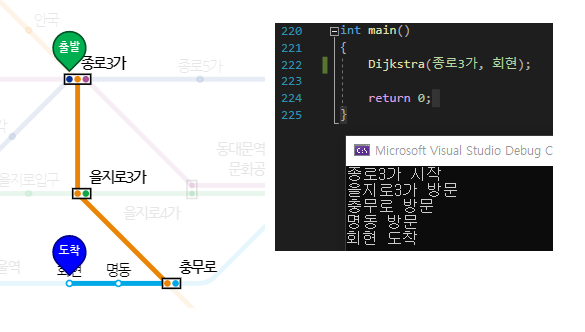
| 다익스트라(Dijkstra) 알고리즘 _ 지하철 노선도 경로 찾기 코드 (2) | 2020.04.05 |